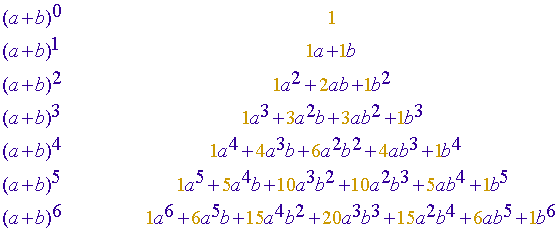Binomische Formeln

Tipp 1

Merke dir die Begriffe: Polynom und Binom.

Jede Subtraktion kann als Addition aufgefasst werden. So gilt z.B. 5a-3b = 5+(-3b)
Algebraische Summen werden als Polynome bezeichnet.
z.B. 3a+4b-3c²+2 oder 5x³-2y

Wenn die Summe nur aus zwei Summanden besteht, spricht man von einem Binom.
Das Polynom 5x³-2y ist beispielsweise ein Binom.
Weitere Beispiele für Binome sind: 3a-2b oder 16u³+12v

Tipp 2

Wichtig ist zu wissen, dass Polynome sich multiplizieren lassen.
Du kannst beispielsweise (3v-2w)²=(3v-2w)·(3v-2w) rechnen. Hier wird das Binom (3v-2w) mit sich selber multipliziert, es handelt sich um einen Sonderfall.

Die binomischen Formeln zeigen drei wichtige Sonderfälle:
I	(a+b)² = (a+b)(a+b) = a²+2ab+b²
II	(a-b)² = (a-b)(a-b) = a²-2ab+b²
III	(a+b)(a-b) = a²-b²

Tipp 3

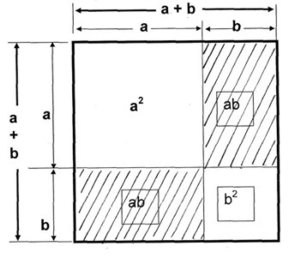
Die erste binomische Formeln kann man gut mit dem Rechteckmodell veranschaulichen:
I	(a+b)² = (a+b)(a+b) = a²+2ab+b²

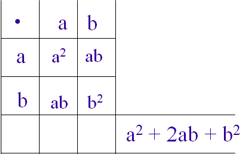
Auch mit Hilfe des Malkreuzes kann man die Multiplikation nachvollziehen.

Tipp 4

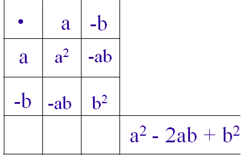
Erstelle für die 2. und 3. binomische Formel selber ein Malkreuz und kontrolliere sie.
II	(a-b)² = (a-b)(a-b) = a²-2ab+b²

III	(a+b)(a-b) = a²-b²

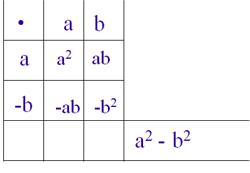
Hinweis 5

Mit Hilfe der binomischen Formeln kannst du nun Produkte berechnen:

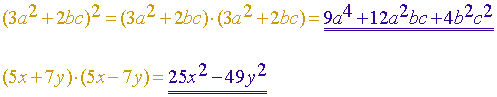
Oft ist die umgekehrte Situation gegeben:
Eine Summe soll als Produkt von Faktoren dargestellt werden.

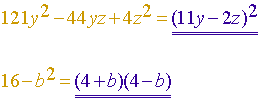
Tipp 6

Kennst du den Zusammenhang zwischen den binomischen Formeln und dem Pascal′schen Dreieck? Das Pascal′sche Dreieck enthält die Binomialkoeffizienten. Sie sind im Dreieck so angeordnet, dass ein Eintrag die Summe der zwei darüber stehenden Einträge ist.